Como antecedentes se tiene que la transformada de
Laplace se puede utilizar para el análisis de señales y sistemas en tiempo
continuo. Un método operacional equivalente para el estudio de sistemas de
ecuaciones deferenciales de tipo lineal discreto, es el método de la
Transformada Z (TZ). Es decir que la TZ está basada en la serie de Laurent y
tiene como objetivo, resolver problemas de señales y sistemas discretos
Lineales Invariantes en el Tiempo (LIT).
De modo general la transformada Z se representa de la
siguiente forma:
Se puede demostrar que para:
La
transformada Z, al igual que otras transformaciones integrales, puede ser
definida como una transformada unilateral o bilateral.
Transformada
Z bilateral:
La TZ
bilateral de una señal definida en el dominio del tiempo discreto x[n]
es una función X(z) que se define
Donde n
es un entero y z es, en general, un número complejo de la forma

Donde A es el módulo de z, y ω es la frecuencia angular en
radianes por segundo (rad/s).
Transformada
Z unilateral:
De forma
alternativa, en los casos en que x[n] está definida únicamente
para n ≥ 0, la transformada Z unilateral
se define como:
En el procesamiento de señales, se usa esta definición cuando la señal es causal. En
este caso, la Transformada Z resulta una serie de Laurent, con ROC
del tipo:
; es decir que
converge "hacia afuera".
La ROC de una transformada X(z) es el conjunto de todos los valores de la variable compleja z para los que X(z) es finita:

El par transformado no es único hasta que no se añade la información relativa a la ROC. Por ello, las tablas de pares z-transformados incluyen una tercera columna con su información de la ROC.
Un ejemplo
interesante de la TZ unilateral es la función de generación de probabilidades,
donde x[n] es la probabilidad que toma una variable discreta aleatoria en el
instante n, y la función X(z) suele escribirse como X(s),
ya que s = z−1. Las propiedades de las transformadas Z son
útiles en la teoría de la probabilidad.
Propiedades de la ROC.
- La Transformada X(z) junto con la ROC definen de forma inequívoca la secuencia x[n], es decir, sin la información de la ROC, existe indeterminación en el cálculo de la antitransformada.
- La ROC de cualquier secuencia tiene simetría circular en torno al origen sobre el plano Z, porque la convergencia sólo depende de .
- La ROC no puede contener polos porque, por definición, la evaluación de X(z) sobre un polo produce divergencia.
- La ROC de secuencias de duración finita (sin polos) es todo el plano complejo, con algunas excepciones.
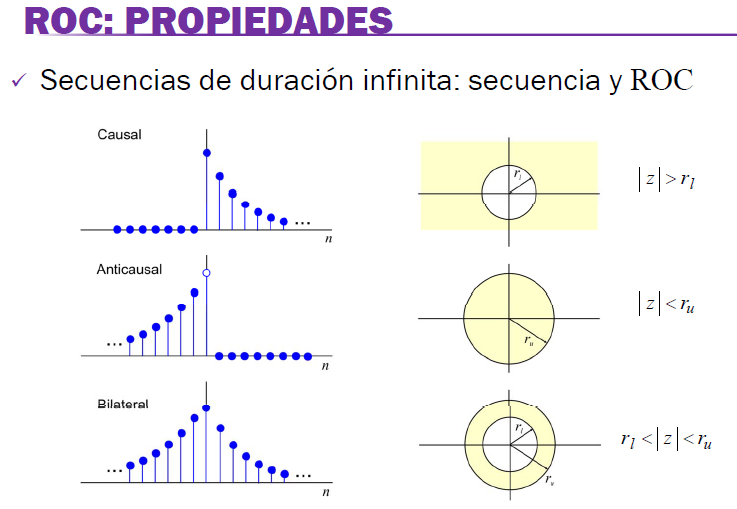
- La ROC de una secuencia (estrictamente) anticausal (con valores nulos en semieje n-positivo) es el interior de una circunferencia.
- La ROC de una secuencia (estrictamente) causal (con valores nulos en semieje n-negativo) es el exterior de una circunferencia.
- La ROC de una secuencia bilateral (combinación de causal o estrictamente no causal) puede ser:
- Una corona circular (si radio parte causal menor que radio parte anticausal)
- No existir (si radio parte causal mayor que radio parte anticausal y no hay intersección)
Ejemplos
ANOTACIONES IMPORTANTES:
𝑗 = √−1; 𝑗^2 = −1; 1/𝑗
= −j
𝑒^(𝜃𝑗) = 𝐶𝑜𝑠 𝜃 + 𝑗 𝑆𝑒𝑛 𝜃 ⟹ 𝑒^(−𝜃𝑗) = 𝐶𝑜𝑠 𝜃 − 𝑗 𝑆𝑒𝑛 𝜃
Si Sumamos: 𝑒^(𝜃𝑗) + 𝑒^(−𝜃𝑗) = 2 𝐶𝑜𝑠 𝜃 ⟺ 𝐶𝑜𝑠 𝜃 = (1 /2)^(𝑒^(𝜃𝑗) + 𝑒^(−𝜃𝑗))
Si Restamos: 𝑒^(𝜃𝑗) − 𝑒^(−𝜃j) = 2𝑗 𝑆𝑒𝑛 𝜃 ⟺ 𝑆𝑒𝑛 𝜃 = (1/2𝑗)^(𝑒^(𝜃𝑗) − 𝑒^(−𝜃𝑗))
Número Complejo: 𝑟 (𝑎 + 𝑏𝑗) = 𝑟 (𝐶𝑜𝑠 𝜃 + 𝑗𝑆𝑒𝑛 𝜃) = 𝑟𝑒^(𝜃j)
𝑟 = √(𝑎^2 + 𝑏^2); 𝜃 = 𝑎𝑟𝑐𝑡𝑎𝑛 (
𝑏/𝑎
)
𝑒 ^(±𝜃𝑗) = 𝐶𝑜𝑠 𝜃 ± 𝑗 𝑆𝑒𝑛 𝜃











